05. 尼柯尔斯图的绘制和分析

尼柯尔斯图的绘制和分析

尼柯尔斯图的绘制

使用奈奎斯特曲线与M环和N环交点来求闭环传递函数的幅频响应和相频响应的缺点是M环和N环都没有以对数形式给出，难以求其增益。尼柯尔斯图是一种从波特图得到灵感、改进M环和N环绘制的图像，如下图所示：

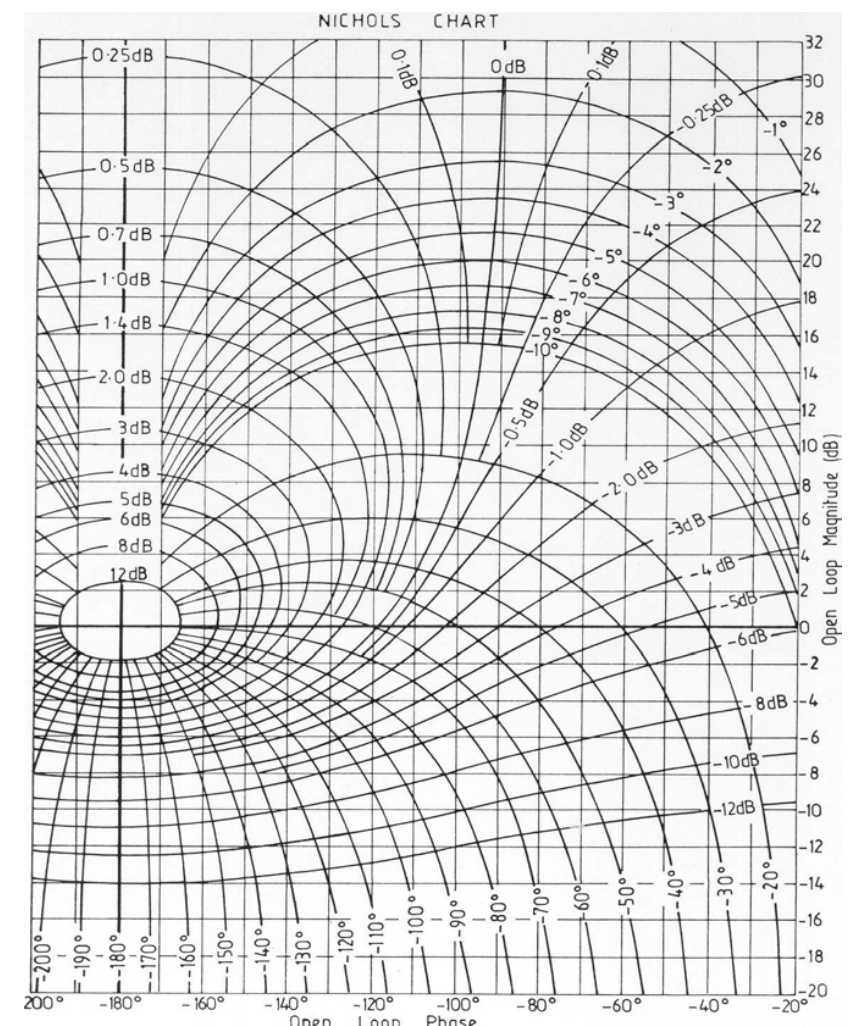
尼柯尔斯图由两部分构成： - 线性坐标表示开环传递函数的幅值和相位，其中横轴表示开环相位，纵轴表示开环幅值。
- 非线性坐标表示M环和N环，M环的每条曲线以分贝值作为标识，N环的每条曲线以角度作为标识。

绘制尼柯尔斯图的步骤

• 将\(G(s)\)转化为\(G(jω)\)，并分离实部和虚部。
  
• 利用定义得到相频响应\(∠G(jω)\)和幅频响应\(|G(jω)|\)。
  
• 列表，从\(ω=0\)开始找到每一个\(ω\)对应的幅值(dB)和相位。

注意\(arctan()\)是一个周期为180°的周期函数，因此可以通过±180°对运算结果进行调整，使得运算结果可以落在尼柯尔斯图的横轴范围上。

• 找到\(ω=∞\)对应的幅值(dB)和相位.
• 在尼柯尔斯图的直角坐标上找到对应的点，连接成线
• 标出\(ω=0\)和\(ω=∞\)的位置。

在MATLAB中，可以使用命令nichols()绘制系统的尼柯尔斯图。

使用卡西欧计算器fx-991CN X辅助绘制尼柯尔斯图/波特图

1. 开机，按【菜单/设置】键进入菜单，按【7】进入表格模式
   
2. 表格模式中显示\(f(x)\)，输入\(20lg|H(jω)|\)的表达式，其中\(ω\)以【\(x\)】表示，输入完成后按【=】键
   
3. 按【SHIFT】键后按【菜单/设置】键进入设置，按【2】后选择【1】将计算模式调整到角度制（D）
4. 显示\(g(x)\)，输入\(arctan(∠H(jω))\)的表达式，其中\(ω\)以【\(x\)】表示，输入完成后按【=】键
5. 显示“表格范围”，设置\(x\)的取值范围，使用【↑】【↓】选择输入对象，输入合适的开始值、终止值和步长，每一项输入完成后按【=】键
   
6. 按下【=】键，计算器会得出从起始值到终止值，每隔一个步长的\(x_i\)所对应的\(f(x_i)\)和\(g(x_i)\)，根据此进行作图
   

• 如果发现得到的\(g(x)\)不在尼柯尔斯图的横坐标范围内，则需要按【AC】键后按【↓】键退回到\(g(x)\)的设置，将表达式调整180°的倍数\(arctan(∠H(jω))±180°\)，（角度符号可以由在\(g(x)\)界面按【OPTN】键后按【2】再按【1】选择）重复上述步骤。

尼柯尔斯图的分析

幅值裕量和相位裕量

尼柯尔斯图上的幅值裕量为-180°时的幅值到0dB的距离。
相位裕量为-180°到0dB时的相位的距离。
通过相位裕量和幅值裕量的分布可以判断系统的稳定性，如下图所示：

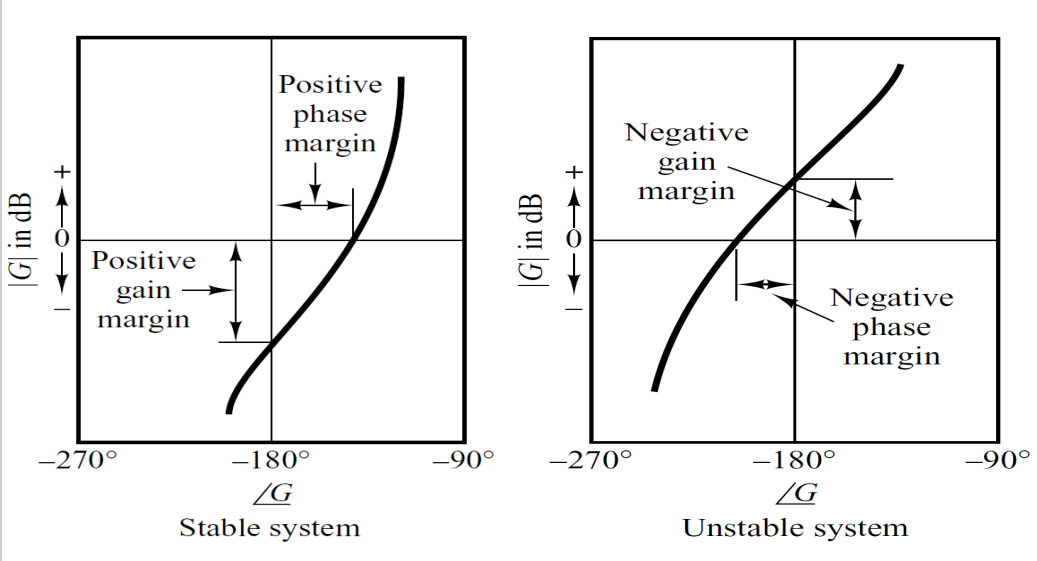
闭环幅频响应和相频响应

只需要找到尼克尔斯曲线与M环和N环的交点，分别连线即可。